Excel 数値の四捨五入、切り捨て、ROUND関数と関連する関数

INDEX

1. 四捨五入の定番「ROUND関数」をマスター
2. 切り捨てには「ROUNDDOWN関数」を使う
3. 切り上げには「ROUNDUP関数」で対応
4. セルの表示形式では見た目上だけ四捨五入される
5. 端数の処理に使えるその他の関数

四捨五入の定番「ROUND関数」

=ROUND（数値, 桁数）

• ［数値］ ... 四捨五入したい元の数値を指定します。
• ［桁数］ ... 四捨五入して、どの桁まで求めるのかを整数で指定します。

2つめの引数［桁数］は、1つめの引数［数値］の一の位を「0」として、それより大きい桁は負の数、小さい桁は正の数で指定します。ちょっと分かりにくいので、［数値］を「1476.532」とした場合の例を以下の表に示します。

［数値］	1	4	7	6	.	5	3	2
［桁数］	-3	-2	-1	0		1	2	3

仮に［桁数］に「-1」を指定すると、十の位までが求められるように、それより下の桁が四捨五入されます。上記の例なら「1480」が求められるわけです。

すべての［桁数］ごとの結果をまとめると、以下のようになります。

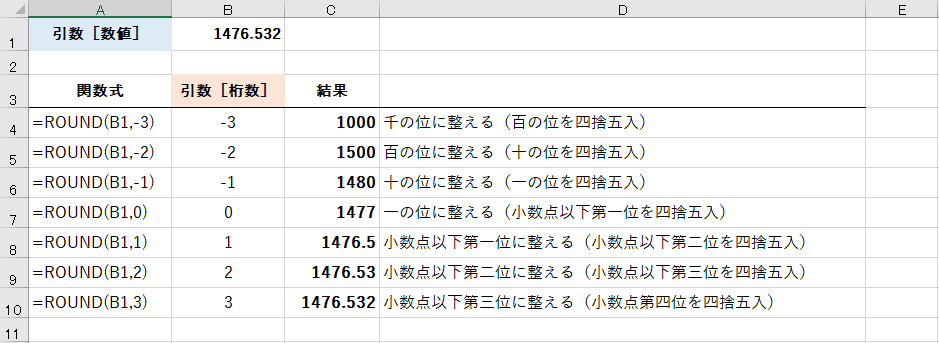
ROUND関数でセルB1の値「1476.532」を四捨五入した結果を表示しています。

ひとまず、［桁数］で「0」を指定したら小数点以下が四捨五入される、と覚えておくといいでしょう。

切り捨てには「ROUNDDOWN関数」

=ROUNDDOWN（数値, 桁数）

ROUND関数との違いは、引数［桁数］で指定した桁よりも下の桁を単純に切り捨てるということです。同様に［桁数］ごとの結果をまとめると、以下のようになります。

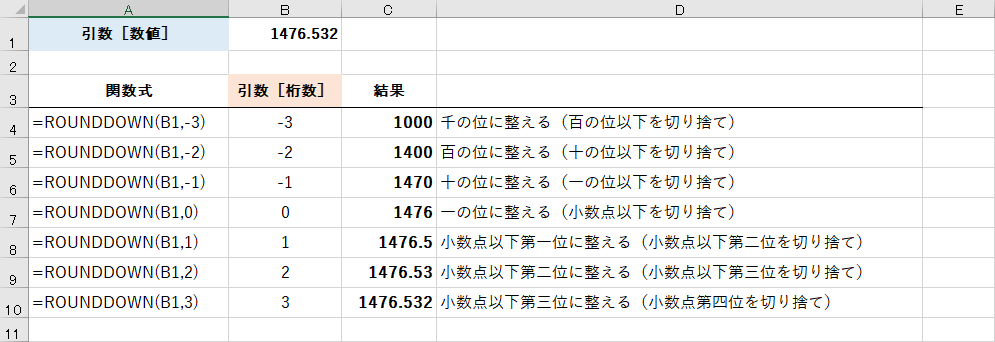
ROUNDDOWN関数では、四捨五入ではなく切り捨てとなっていることが分かります。

切り上げには「ROUNDUP関数」

=ROUNDUP（数値, 桁数）

すべての［桁数］ごとの結果は以下のようになります。指定した桁よりも下の桁が切り上げられた結果が求められています.

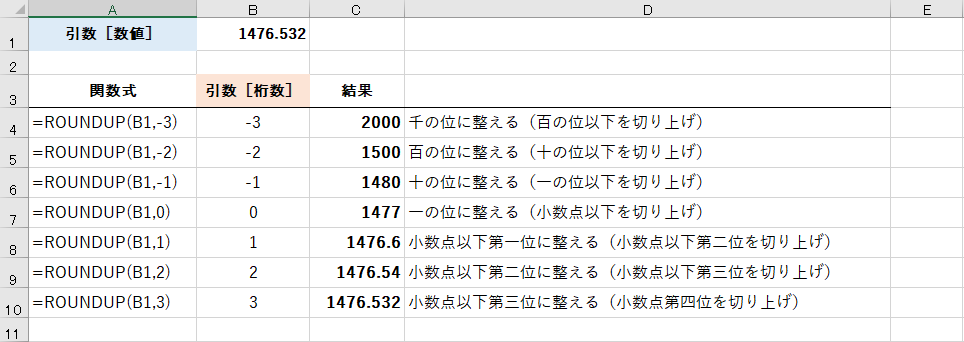
ROUNDUP関数により、セルB1の値「1476.532」が指定した桁で切り上げられています。

セルの表示形式では見た目上だけ四捨五入される

ここまでは関数を使って端数を処理する方法を解説しました。ただ、四捨五入に関しては、関数を使わないもう1つの方法があります。セルの表示形式を使う方法です。

［ホーム］タブの［数値］グループにある［小数点以下の桁数を減らす］ボタンを使うと、小数点以下の桁数を調整し、非表示にした桁を四捨五入できます。

手軽に四捨五入できて便利なのですが、この方法では見た目上の数値が変わるだけで、セルに入力されている実際の数値は変わらないことに注意してください。具体的な例を見てみましょう。

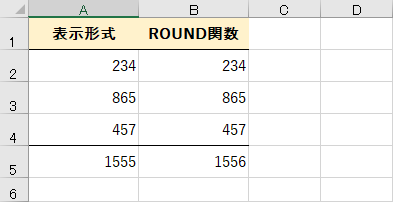
「表示形式」列と「ROUND関数」列で、同じ数値が入力されているように見えます。しかし、5行目で求めている合計が異なっていますね。「234＋865＋457」は「1556」が正しいのですが、なぜこのような現象が起こるのでしょうか？

数式バーで「表示形式」列のセルを見てみると......

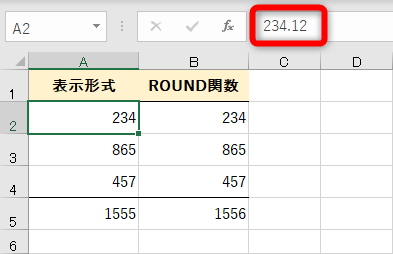
実際には、セルA2に「234.12」と入力されていることがわかります。

一方の「ROUND関数」列はというと......

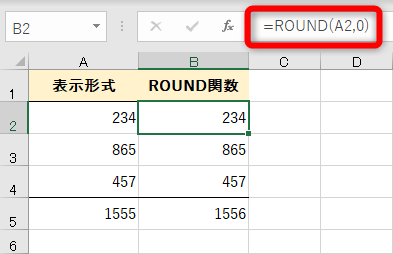
セルB2には「=ROUND(A2,0)」と入力されており、「234.12」の小数点以下第一位を四捨五入した数値が求められています。

ここで［小数点以下の桁数を増やす］ボタンをクリックして......

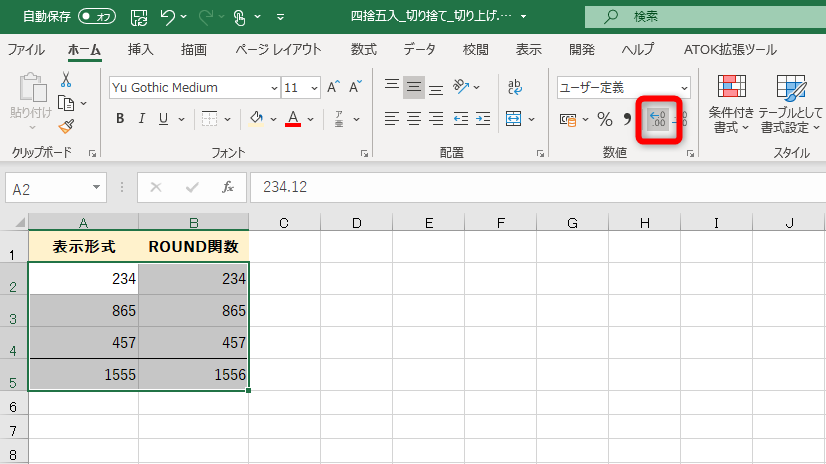
非表示になっていた小数点以下の桁を見てみます。

【エクセル時短】数値の四捨五入、切り捨て、切り上げをおさらい。ROUND関数と関連する関数を理解する | できるネット(新しいタブで開く)

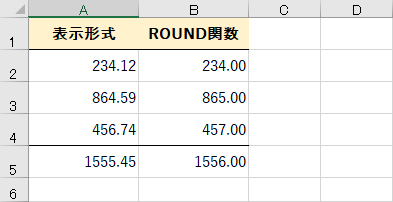
一目瞭然ですね。「表示形式」列の数値には、実際には小数点以下の桁があります。5行目で求められている合計は正しいのですが、セルの表示形式で見た目上だけ四捨五入すると、計算が合わなくなるわけです。

一方、「ROUND関数」列では、関数による計算結果がセルにそのまま入力されているため、見た目と実際の計算が一致します。

引用

できるネットより

https://dekiru.net/article/18663/